Reading and Interpreting Numbers on Logarithmic Scales

Reading and Interpreting Numbers on Logarithmic Axes

When data is plotted on logarithmic scales, the numbers are typically represented with one of two formats.

When plotting a set of numbers represented exponentially by factors multiplied by powers of 10, the numbers can be plotted on a logarithmic axis with major axis intervals corresponding to powers of 10 (e.g. 0.1 or 1 x 10^-1; 1 or 1.0 x 10⁰; 10.0 or 1 x 10¹; etc.) and with minor axis intervals corresponding to 1/10^th, 2/10^th, etc. from left to right of the major axis intervalsl (e.g. 0.2 ,0.3, etc. between major interval 0.1 and 1.0).
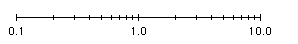
When plotting the a set of numbers represented by their raw logarithmic values on a linear axis with the major axis intervals corresponding to the powers of base 10 (e.g. Log (10^-1) = -1.0; Log 10⁰ = 0.0; Log 10¹ = 1.0; etc.) and the minor axis intervals correponding to 1/10^th, 2/10^th, etc. from left to right of the major axis intervals (e.g. -0.9 ,-0.8, etc. between major interval -1.0 and 0.0).

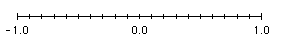
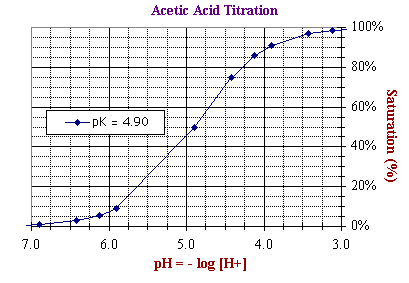
The two scales above cover an identical range of numbers but differ in their utility as illustrated below by the two representations of the titration curve of acetic acid.

When data is plotted on a log axis, each data point or axis corresponds to an exponential number of base 10 ( e.g., 1.0 x 10^-7; 1 x 10^-6; etc., in listing the major axes from left to right).

When the logarithmic values of the data points or the axes are plotted on a linear axis, each data point or axis corresponds to a raw logarithmic value (e.g., 7.0 correponds to the -log (10^-7); etc).

Both graphs represent exactly the same data. In other words, they are there quantitatively equivalent. However, the different formats provide easy access to different types of information about the titration. For example:

By using the top plot, [H⁺] can be read directly from the X-axis; for example, at 45% saturation, [H⁺] = 1.0 x 10^-5.
By using this bottom plot, [H⁺] must be calculated by taking the antilog of the negative value of the log value read from the X-axis; for example, at 45% saturation, [H⁺] = antilog (-5.0) = 10^-5.
In contrast, the bottom plot is easier use for determining the pK_d of acetic acid, defined as the negative log of the dissociation constant, or -log ([H⁺]_50%) with [H⁺] at Ya = 50% saturation. As read directly from the X-axis of the bottom plot, pKdn = 4.90, where Ya = 50% saturation.
With the top plot, the value read for [H⁺] at 50% saturation from the X-axis -- i.e., 1.25 x 10^-5 -- must be convert to the negative of its log value;
i.e., pKdn = - log (1.25 x 10^-5) = - log (1.25) - log (10^-5)
= - log (1.25) + 5 = - log (5/4) + 5 = - log (5) + log (4) + 5
= - 0.7 + 2 x 0.3 + 5 = - 0.7 + 0.6 + 5 = - 0.1 + 5 = 4.9 = pKdn

©	Duane W. Sears Revised: April 9, 2019